skip to main |
skip to sidebar
Κυριακή 22 Απριλίου 2012
Τετάρτη 18 Απριλίου 2012
"Καλή Ανάσταση" από την Σούλα με ευκλείδεια αυγά
Η φίλη και συνάδελφος Σούλα Σούφαρη μου έστειλε μια καταπληκτική κάρτα για τις φετινές Πασχαλινές ευχές της:
Αισθητικά πανέμορφη και μαθηματικά προκλητική! Γιατί το σχήμα του αυγού έχει σχεδιαστεί με έναν απίστευτα έξυπνο τρόπο. Διαβάστε το σχετικό άρθρο στην ιστοσελίδα του Εργαστηρίου Μαθηματικών:
http://mathlab.mysch.gr/filoi/egg.html
Αισθητικά πανέμορφη και μαθηματικά προκλητική! Γιατί το σχήμα του αυγού έχει σχεδιαστεί με έναν απίστευτα έξυπνο τρόπο. Διαβάστε το σχετικό άρθρο στην ιστοσελίδα του Εργαστηρίου Μαθηματικών:
http://mathlab.mysch.gr/filoi/egg.html
Ετικέτες
μαθηματικά και τέχνες,
παιχνίδια,
πλακοστρώσεις
Δευτέρα 16 Απριλίου 2012
Παρασκευή και 13
Φέτος η Μεγάλη Παρασκευή ήταν στις 13 Απριλίου. Δεν ξέρω πόσοι πρόσεξαν την "αποφράδα μέρα", εγώ όμως την πρόσεξα, καθώς αποτελεί ένα από τα αγαπημένα μου θέματα. Όχι το ότι η "Παρασκευή και 13" είναι αποφράδα μέρα - δεν τα πιστεύω αυτά - αλλά το πόσο συχνά αυτή εμφανίζεται στον ημερολογιακό κύκλο.
Τι είναι όμως ο ημερολογιακός κύκλος; Ως γνωστό, η 13 Απριλίου από χρόνο σε χρόνο αλλάζει ημέρα, δεν είναι πάντα Παρασκευή. Όμως, αν δούμε τις ημερομηνίες και τις αντίστοιχες μέρες τους σε διάστημα 400 ετών (τόσος είναι ο ημερολογιακός κύκλος) θα διαπιστώσουμε ότι αυτές επαναλαμβάνονται αυτούσιες και την επόμενη 400-ετία και την μεθεπόμενη κ.ο.κ. Έτσι, στις 13 Απριλίου 2412 θα είναι πάλι ημέρα Παρασκευή, όπως άλλωστε ήταν και στις 13 Απριλίου 1612.
Η περίοδος των 400 ετών οφείλεται σε δύο λόγους: Πρώτον στο ότι η εβδομάδα έχει 7 μέρες και δεύτερον στο ότι ορισμένα έτη από τα 400 είναι "δίσεκτα" έχουν δηλαδή 366 μέρες αντί για 365, όπως το δίσεκτο έτος 2012. Παρένθεση: τα δίσεκτα δεν είναι τα έτη που είναι πολλαπλάσια του 4, αλλά τα έτη που είναι πολλαπλάσια του 4 και δεν είναι πολλαπλάσια του 100. Από αυτά εξαιρούνται τα πολλαπλάσια του 400 που πάλι είναι δίσεκτα. Δηλαδή το 2000 ήταν δίσεκτο, όμως τα 2100, 2200 και 2300 δεν θα είναι δίσεκτα.
Τι είναι όμως ο ημερολογιακός κύκλος; Ως γνωστό, η 13 Απριλίου από χρόνο σε χρόνο αλλάζει ημέρα, δεν είναι πάντα Παρασκευή. Όμως, αν δούμε τις ημερομηνίες και τις αντίστοιχες μέρες τους σε διάστημα 400 ετών (τόσος είναι ο ημερολογιακός κύκλος) θα διαπιστώσουμε ότι αυτές επαναλαμβάνονται αυτούσιες και την επόμενη 400-ετία και την μεθεπόμενη κ.ο.κ. Έτσι, στις 13 Απριλίου 2412 θα είναι πάλι ημέρα Παρασκευή, όπως άλλωστε ήταν και στις 13 Απριλίου 1612.
Η περίοδος των 400 ετών οφείλεται σε δύο λόγους: Πρώτον στο ότι η εβδομάδα έχει 7 μέρες και δεύτερον στο ότι ορισμένα έτη από τα 400 είναι "δίσεκτα" έχουν δηλαδή 366 μέρες αντί για 365, όπως το δίσεκτο έτος 2012. Παρένθεση: τα δίσεκτα δεν είναι τα έτη που είναι πολλαπλάσια του 4, αλλά τα έτη που είναι πολλαπλάσια του 4 και δεν είναι πολλαπλάσια του 100. Από αυτά εξαιρούνται τα πολλαπλάσια του 400 που πάλι είναι δίσεκτα. Δηλαδή το 2000 ήταν δίσεκτο, όμως τα 2100, 2200 και 2300 δεν θα είναι δίσεκτα.
Ας έρθουμε τώρα στην ημέρα της Παρασκευής και 13. Αν στο διάστημα των 400 ετών συγκεντρώσουμε όλες τις "13 του μήνα", συνολικά 400*12=4800 μέρες και δούμε ποιες είναι σε κάθε ημέρα της εβδομάδας, θα διαπιστώσουμε το ακόλουθο:
Ετικέτες
αριθμοί,
εφαρμοσμένα μαθηματικά
Το μπλουζάκι του Περικλή
Ο συνάδελφος Περικλής, καθηγητής Πληροφορικής, έχει πολύ ενδιαφέροντα μπλουζάκια από μαθηματική άποψη, το καθένα και ένα ωραίο πρόβλημα.
Εκείνο το πρωινό, στάθηκα αρκετή ώρα μπροστά του, προσπαθώντας να αποκωδικοποιήσω το δέντρο με τους αριθμούς. Στην βάση ήταν η μονάδα και μετά το 2, το 4, το 8, το 16,... Υπέθεσα ότι οι αριθμοί διπλασιάζονταν. Όμως το 5 μετά το 16 μου "χαλούσε" αυτόν τον υπέροχο κανόνα. Το ίδιο συνέβαινε και μετά: ενώ ακολουθούσαν μερικά βήματα διπλασιασμού, ξαφνικά, "πέφταμε" σε μικρότερο αριθμό: 5, 10, 20, 40, 80, 160, 53...
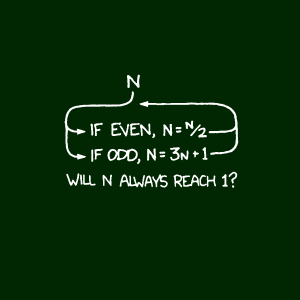
Δεν μπορούσα να εντοπίσω κάποια σχέση. Του ζήτησα να κάνει μεταβολή να δω και την πίσω όψη της μπλούζας. Εκεί υπήρχε ένας κανόνας, που ο Περικλής ψιθύρισε πως ήταν το "σκονάκι" της γριφώδους μπλούζας του: Αν ο Ν είναι άρτιος, τότε Ν=Ν/2. Αν ο Ν είναι περιττός, τότε Ν=3Ν+1.
Τότε μόνο κατάλαβα ότι διάβαζα "ανάποδα" το δέντρο. Δεν έπρεπε να ξεκινώ από την ρίζα του, αλλά από τις πάνω άκρες των κλώνων του, που κάθεμιά φιλοξενούσε και έναν τυχαίο φυσικό αριθμό. Αν ο αριθμός ήταν άρτιος, ο αμέσως πιο κάτω ήταν το μισό του, ενώ αν ήταν περιττός, ο αμέσως πιο κάτω ήταν ο τριπλάσιός του αυξημένος κατά μια μονάδα. Με αυτόν τον τρόπο δημιουργείται μια ακολουθία αριθμών, ο κλώνος ολόκληρος.
Αλλά δεν θα είχαμε το μπλουζάκι, ούτε εγώ θα έγραφα την ανάρτηση, αν το 1937 ο Lothar Collatz δεν διατύπωνε την εικασία (εικασία Collatz) ότι με την διαδικασία αυτή, ανεξάρτητα από ποιον φυσικό αριθμό Ν ξεκινάμε, καταλήγουμε πάντα στην μονάδα, την ρίζα του δέντρου!
Εκείνο το πρωινό, στάθηκα αρκετή ώρα μπροστά του, προσπαθώντας να αποκωδικοποιήσω το δέντρο με τους αριθμούς. Στην βάση ήταν η μονάδα και μετά το 2, το 4, το 8, το 16,... Υπέθεσα ότι οι αριθμοί διπλασιάζονταν. Όμως το 5 μετά το 16 μου "χαλούσε" αυτόν τον υπέροχο κανόνα. Το ίδιο συνέβαινε και μετά: ενώ ακολουθούσαν μερικά βήματα διπλασιασμού, ξαφνικά, "πέφταμε" σε μικρότερο αριθμό: 5, 10, 20, 40, 80, 160, 53...
Δεν μπορούσα να εντοπίσω κάποια σχέση. Του ζήτησα να κάνει μεταβολή να δω και την πίσω όψη της μπλούζας. Εκεί υπήρχε ένας κανόνας, που ο Περικλής ψιθύρισε πως ήταν το "σκονάκι" της γριφώδους μπλούζας του: Αν ο Ν είναι άρτιος, τότε Ν=Ν/2. Αν ο Ν είναι περιττός, τότε Ν=3Ν+1.
Τότε μόνο κατάλαβα ότι διάβαζα "ανάποδα" το δέντρο. Δεν έπρεπε να ξεκινώ από την ρίζα του, αλλά από τις πάνω άκρες των κλώνων του, που κάθεμιά φιλοξενούσε και έναν τυχαίο φυσικό αριθμό. Αν ο αριθμός ήταν άρτιος, ο αμέσως πιο κάτω ήταν το μισό του, ενώ αν ήταν περιττός, ο αμέσως πιο κάτω ήταν ο τριπλάσιός του αυξημένος κατά μια μονάδα. Με αυτόν τον τρόπο δημιουργείται μια ακολουθία αριθμών, ο κλώνος ολόκληρος.
Αλλά δεν θα είχαμε το μπλουζάκι, ούτε εγώ θα έγραφα την ανάρτηση, αν το 1937 ο Lothar Collatz δεν διατύπωνε την εικασία (εικασία Collatz) ότι με την διαδικασία αυτή, ανεξάρτητα από ποιον φυσικό αριθμό Ν ξεκινάμε, καταλήγουμε πάντα στην μονάδα, την ρίζα του δέντρου!
Ετικέτες
αριθμοί,
εφαρμοσμένα μαθηματικά,
μαθηματική έρευνα
Ετικέτες
- αριθμοί (7)
- εκπαίδευση (9)
- επιφάνειες (5)
- εφαρμοσμένα μαθηματικά (19)
- θεωρητικά μαθηματικά (1)
- μαθηματικά και τέχνες (12)
- μαθηματική έρευνα (7)
- παιχνίδια (12)
- πλακοστρώσεις (6)
- πολύεδρα (2)
- Πράξεις αριθμών (2)
- συμμετρίες (3)
- τεχνολογία (12)
- φιλοσοφία (4)
Αρχειοθήκη Ιστολογίου
-
►
2013
(4)
- ► Φεβρουαρίου (1)
- ► Ιανουαρίου (1)
-
▼
2012
(11)
- ► Δεκεμβρίου (1)
- ► Ιανουαρίου (1)
-
►
2011
(13)
- ► Σεπτεμβρίου (1)
- ► Φεβρουαρίου (1)
Αναγνώστες
Σελίδες
2009 - Μαθηματικές Πτήσεις. Powered by Blogger
Blogger Templates created by Deluxe Templates
Wordpress Themes developed by Templatelite.com
Blogger Templates created by Deluxe Templates
Wordpress Themes developed by Templatelite.com